New statistics for design researchers
A Bayesian workflow in tidy R
2021-12-23
1 Introduction
1.1 Whom this book is for
Are you a design researcher? Is your work about improving computer software, cars, medical devices, services or trainings? Are you using data for your work, in order to measure or compare how well a design works? Welcome to the club!
Of course, I have no idea who you are, personally, but I figure you as one of the following types:
You are an Human Factors researcher, thirty-three years old, leading a small team in the center for research of a German car manufacturer. Your task is to evaluate emerging technologies, like augmented reality, car-to-car communication and smart light. Downstream research relies on your competent assessment of what is feasible. For example, you have just been asked to evaluate whether blue light can make for safer driving: Blue light makes people wake up easier. Could this also be used to let car drivers not fall asleep? You are working together with two engineers and a student of industrial design. Your plan is to put a light color device into a prototype car. Two workstation are stuffed into the boot of the car for record physiological signals and driving performance. This all is very expensive and someone is paying for it. Your skin is in the game.
Or, you are a young academic and just got a cum laude master’s degree in computer science. For your thesis you developed and implemented an animated avatar for a digital assistant. A professor from the social psychology department has read your thesis. She just got funding for a project on mass emergency communication using projected virtual characters. Being afraid that a psychologist researcher would not be up to the technical part of the project and found you. But, you ask yourself, am I up to the task of running experimental studies and do the statistics?
Or, you are a student in some applied field of Psychology and your thesis project is about evaluating a design, or a training, or a therapeutic intervention, or making this world a better place in any other way. From your bachelor studies, you already have a background in Statistics, but it occurs to you, the basics won’t do it for what you have in mind.
Finally, perhaps you are an experimentalist. Are you doing research with people, but your research question addresses the human mind, in general, and the answers you seek are far from being applicable to anything in sight. You are not a design researcher, but don’t put this book away too fast! The only difference between a design experiment and a psychological lab experiment, is in the different stakes, not the research design and structure of data. In cognitive experiments, a drop in reaction time can mean that some priming or learning has occured, which can either strengthen or defeat a certain theory on human cognition. In a design experiment, if users can work faster with one interface compared to another, that is usually a good thing. For a statistical model, intentions don’t matter. Chances are good that you will be able to read through the ephemeral details of the design research cases I present and apply the same methods to your own research situations.
1.2 Quantitative design research
A design is the structure of an artifact (or a process) that someone conceived for a purpose. This definition is extremely broad as it covers everything, tea kettles, software, cockpits, training programs and complex human-machine systems. The only exception I can think of is art, which is not design, because purposefulness is a requirement. Quantitative design research simply is about measuring to what extent a design, a class of designs or a design feature fulfills its purposes. We all have purposes and much of the time it is quite a job to get there. Getting-there typically requires resources and often we have to strike some sort of balance. The two basic questions in quantitative design research are:
- To what extent does a design fulfill its purpose?
- What are the costs for the design?
A good design simply fulfills its purpose enough to justify the costs. The methods and examples in this book all deal with the first question. Quantitative design research practically always is an evaluation of some sort. This evaluation can either be very specific, such as the effect of a new or changed feature in A/B testing, or generic, such as the uncanny effect of human-likeness of robot faces on the feelings of people. Broadly, the purpose of specific design study is to evaluate the fitness of a single design, before it enters the next development stage (or is rolled out to the users). In contrast, generic design studies have the purpose to inform future designs of a class. In both cases, something is at stake, immediately or in the future, and this is why quantification is required.
Quantification happens on two levels: the research questions and measures. In most research, a process called measurement produces numbers. This can be as simple as the reaction time to a signal, or as advanced as a trained neural network that judges the emotional content of tweets.
For calling a study quantitative research it is required to ask quantitative research questions. In the real world, decisions are (or should be) based on benefits and rational allocation of resources. Changing the background color of a website might just be a switch (and can have undesired effects as users hate change), but restructuring an intranet site can be very costly. In industrial design research, there usually is someone who wants to know whether this or that redesign is worth it, and that requires to ask research questions like the following examples:
- By how much does reaction time degrade with age and it is safe that people beyond 80 still drive?
- Does design B reduce the required number of steps by a third, at least?
- What proportion of users prefers red over yellow? All websites better go red?
Sadly, in much existing research, the quantitative perspective is frequently lost along the way and conclusions read more like:
- Older people have longer reaction times in traffic situations (\(p \leq .05\)).
- People find information more easily with design A, compared to B (\(p \leq .05\)).
- Chinese people on average prefer red color schemes over yellow (\(p \leq .001\)).
There simply is no numbers in these statements (except for the notorious p-values, which I will briefly discuss in chapter 3). The statistical methods introduces in this book do a terrific job at drawing quantitative conclusions. Every regression model features a so called outcome, which must be a measure (rather than a category).
Modern designs tend to be very complex and so are research questions, potentially. The options for designing just your personal homepage are myriad and there is considerable uncertainty about which feastures, or rather which configuration of features works best. Consider every option, say font type, font size, color, background color, position of menu, a potential impact factor on how pleasant the page is to read. At the same time, these features are not independent. For a simple example, readability of a website depends on font size and contrast, which means you can trade in one for the other. Perhaps, someone should once and for all figure out the optimal configuration. Such a study would require, that as many as possible impact factors are represented in a single study and evaluated by a single comprehensive statistical model. The models introduced in thios book handle such complexity with grace. There is theoretically no limit for the number of impact factors or predictors.
The central peculiarity in all behavioural research is that measures are extremely noisy, with the consequence that we can never draw totally firm conclusions. In chapter 3, the concept of uncertainty will be elaborated upon, but for now it suffices to understand that no statistical models can make fully certain predictions. Imagine a simple test for cognitive processing speed. Participants wait for a signal and react to it. Although the task is the same every time, the measures most likely will be scattered, like 900ms, 1080ms, 1110ms. Imagine further this were an ability test in a training for, say, astronauts. To be admissioned to the space program the applicant needs a score of less than 1000ms. Would you dare to decide on the career of a young person based on these three observations? Hardly so. Uncertainty can be reduced by taking more measures, but 100% certainty can never be reached. The approach presented in this book address teh uncertainty problem by making the level of uncertainty transparent.
In contrast, consider measuring a persons waste length for the purpose of tayloring a suit. By using a meter, the taylor measures 990mm, and would be perfectly fine with that. Why did the taylor not take a second and a third measure? Well, experience tells that meters are pretty precise measures and waste length shows relatively little variation (under constant habits). Say the two measures were 995mm and 989mm. Such small deviations have practically no influence on cutting the linen.
“Our minds are not run as top - down dictatorships ; they are rambunctious parliaments, populated by squabbling factions and caucuses, with much more going on beneath the surface than our conscious awareness ever accesses.”
Carroll, Sean. The Big Picture (Kindle Locations 5029-5031). Oneworld Publications. Kindle Edition.
Vast fluctuations of measures are common in design research, simply for the fact that human behaviour is involved. Every magnitude we derive from a study is uncertain to some degree. Uncertainty makes that at any moment, we can rely on a quantitative result only to some extent, which influences how we take risks. New Statistics solves this problem by attaching a degree of uncertainty to every effect. Section 3.1 gives some reasoning and examples, how to operate rationally under uncertainty, and drives you right into the arms of Bayesian statistics.
When you have no greater goal in mind than proving your design is of quality, user studies are effective and quick means. In the easiest case, you want to put your design against a fixed benchmark. For example, in the design of automotives, media devices in the cockpit may not distract the driver for more than 1.5 seconds at times. If you want to prove that a design complies to this rule, you will have to plug some advanced eye tracking gear into a prototype car and send people on the test drive. But once the data is in, things get really simple. The saccade measures directly represent what you were out for: the length of episodes of visual attention on the media display. In web design, it is common to compare two or more designs in order to make the best choice. An e-commerce company can put a potential future design on the test drive, delivering it to a customer sample. Performance is measured as hard currency, which is as close to the purpose as it can get.
A user studies solves the momentary problem of comparing a local design to a benchmark (which can be another design). In the long run, design configurations are too manyfold to be compared in a one-by-one manner. It is inevitable that we try to trace some general patterns and apply our knowledge to a whole class of designs at once. Our research design just got one step more complex. Instead of just checking whether a smaller font size creates problems on a single website, the reseacher reaches out to comparing the combined effect of aging and font size on reading time, in general. This is what I call a design experiment.
Design experiments allow for much broader conclusions, if done right, but there are a some issues:
- The design features under scrunity must be under control of the researcher. It does not suffice to collect some websites with varying font sizes, but every website needs to undergo the test at various font sizes.
- The design feature must undergo a full range of manipulations. You will not find the laws of readability by just comparing 10pt versus 12pt.
- Design features usually do not stand on their own. Readability is influenced by other factors, such as contrast and comprehensibility. Deriving a model from just one design will only generalize to this one design. Hence, the researcher must run the experiment on a sample of designs, with one of two strategies (or a mix of both): the randomization strategy takes a representative sample of designs, hoping that other impact factors average out. As we will see in 5.4, this is a daring assumption. Therefore, the preferred way is statistical control, where potential impact factors are recorded and added as control variables to the regression model.
The parameters for decision making vary with the purpose. In an admission test for astronaut training, a decision is raised on individuals. Also, there is only this one shot, figuratively and literally, and the costs are enormous. Down on earth, many designs affect many people at once, sometimes in the billions, if just a little bit. Consider any commercial or informational website. If you decide, for aesthetic reasons, to shrink the font size, it is not unlikely, that you just start loosing all visitors from the e-senior generation. Or, if your content is really good, they may swallow the bitter pill and start using looking glasses on their O-pads. As a researcher, you can approach any of these problems by a specific user study or a generic design experiment.
Effective design research hinges on many methodological considerations, such as selection of valid measures, efficient experimental designs and sampling schemes. To keep this confined in a textbook on statistical models, I will briefly address measures in the following chapter. Experimental design will not explicitly being addressed, but all real case studies used in this book have been carefully designed and I am confident to offer them as templates for your own research.
1.3 What is New Statistics?
New Statistics is neither novel, nor are the contained methods truly bleeding-edge. The term has been coined by (Cumming 2013) and it is new in two respects: first, what can be subsumed as Classic Statistics is a zoo of crude tools from the first half of the 20th century. Second, NewStats and ClassicStats take different perspectives. ClassicStats emphasizes the approach of testing hypotheses, that were derived from theories, which is known as null hypothesis significance testing (NHST). New Statistics is about quantification of impact factors.
The difference is best illustrated by seeing how in either one the results are reported. A classic analysis report has the following structure:
Recollect the hypothesis: Participants in the control condition are faster.
Descriptive statistics: The difference of means in the sample is \(217\).
State the null hypothesis: \(H_0: (M_\textrm{exp} - M_\textrm{control}) = 0\)
Test the assumptions of ANOVA:
- homogeneity of variance
- Normal distribution of residuals
If assumptions are not violated, continue with ANOVA, otherwise with a non-parametric test.
Report p-values: The chance that a difference of \(217ms\) happens, when the null hypothesis is true, is \(p \leq .05\)
… proceeding to the next research question and repeat the cycle
A New Statistics report has the following structure:
- Collect all research questions: Participants in the experimental condition are 10% faster and Older participants are slower.
- Explorative figures: The boxplot shows that participants with the novel design are faster by around 200 seconds on average. and The scatterplot shows a positive trend with age.
- Reasoning about the measures and shape of randomness: Response time are strictly positive and frequently left-skewed.
- Building one model: We use a model on response time with two predictors, Condition and age, with Exponential-Gaussian distributed responses.
- Reporting quantities with uncertainty: The novel design leads to faster reaction times, with a best guess of 205 ms difference. With 95% certainty, the true difference is at least 172 ms
The first to note is that in New Stats research questions are quantitative. For the design researcher it is essential to know how large an improvement is, because design always takes place in a web of trade-offs. Let’s take the example of putting blue light into cars, to keep drivers awake. It is one thing to test that on a test drive or a simulator, it is another to kick it off into development and produce a car series. That means that applied or industrial researchers eventually have to report their results to decision makers and the data must ascertain not only that there is an improvement, but that the improvement justifies the costs.
In New Statistics we have a much higher flexibility in designing statistical models. Classic models are like a zoo, where most animals cannot interbreed. You can find an animal that is furry, another one that has green color and a third one that can swim. But, you cannot cross them into one animal that does it all. New Statistics is like modern genetics, where properties of animals are encoded on basic building blocks. Theoretically, once you understand the basic building blocks, you can assemble the animal you want. In our favor, the building blocks of statistical models have long been understood and they are just a few. This book covers the family of Generalized Linear Multi-level Models, which consists of the following building blocks
- A linear relation describes the basic quantitative relationship between a metric predictor and a metric outcome.
- By dummy coding, categorical (i.e. non-metric) predictors can be used, as well.
- By linear combination, the simultaneous effect of multiple predictors can be modelled.
- Random effects apply for categorical variables, where the levels members of one population.
- Multi-level modelling allows the simultaneous estimations on population-level and participant-level.
- Link functions linearizes the predictor-outcome relationship for outcomes which have boundaries (which they all do).
- Error distributions adjust the shape of randomness to the type of outcome variable.
The power NewStats model lies in the combinatoric explosion arising from the full interoperability of its building blocks.
The most powerful building block is the combination of linear terms.
A linear model for the effect of blue light would be written as RT ~ Light.
To simultaneously address the age effect, we had to write just RT ~ Light + age.
In New Statistics, statistical models are not pulled off the shelf, but are designed in a thoughtful manner, based on an analysis of the data-generating process.
I wouldn’t go so far as to say, we are only scratching the surface with the family of GLMM, but there definitely are more building blocks, that further expand the family of models, for example, also allowing non-linear relationships (see 5.5 and 7.2.1.2). New Statistics does not require the GLMM family per se, it only requires that models have a quantitative interpretation. That includes the whole set of models commonly referred to as parametric models, of which GLMM is one class.
If there are parametric models, what about non-parametric models? In ClassicStats, non-parametric tests are routinely used as a fall-back for when none of the few available parametric models sits well. Non-parametric methods are banned from NewStats, for two reasons: first, they don’t give quantitative answers. Second, they are not needed. When reaction times are not “distributed Normal,” the researcher can simply swap the building block that defines the shape of randomness. Or even better: the researcher knows that reaction times are not Normal and selects an appropriate response distribution right away. Infamously in ClassicStats, non-parametric tests are often misused to check the assumptions of a model, like the Normality assumption. New Statistics does not require such crude tricks. The process of assumption checking (and being screwed if any are violated) is simply replaced by a top-down knowledge-driven model design.
Finally, ClassicStats and NewStats models differ in what pops out of them. The very reason to run a statistical model, rather than pulling the answers from descriptive statistics, like group averages, is that data obtained from a sample is never a complete picture, but is always tainted by some degree of uncertainty. In ClassicStats, questions are posed as binary (Yes/No), following the traditional method of null hypothesis significance testing: Is there a difference, or not? Awkwardly, the way a null hypothesis is posed does not seem to focus on the difference, but on the opposite: Imagine, there really were no difference. How likely would the observed data be? If we were to repeat the experiment a hundred times, how often would we see such a result? If this blurs your mind, you are not alone. Where do all these experiments come from? In fact, the p-value is just a clever mathematical trick to extrapolate from the data at hand, to what would happen with an infinite number of replications. While we could view the so called alpha error as a continuous measure of certainty, it is not a measure of how strong an effect is. Instead, the p-value is a convolution of effect size, noise level and sample size. That makes it very difficult to interpret, which is most apparent with the mal-practivce of non-parametric tests for assumptions checking: If the data set is small, even large deviations from, say Normality, will not be detected. On large data sets the opposite happens: minor deviations lead to the rejection of a reasonable approximation. In practice, the p-value is not even used as a continuous measure, but is further simplified by a social norm: If the p-value is smaller then 5%, the null hypothesis is rejected, if it is not, we are in the limbo.
New Statistics asks quantitative questions and our models produce quantitative answers, together with levels of uncertainty. These answers come as parameter estimates, like the difference between two groups. Estimates are uncertain and it is common, to express the level of uncertainty as intervals that contain the true value with a probability of 95%. This can be customized in various ways, which is immensely useful in decision-making situations.
In this book I am advocating the Bayesian approach for doing New Statistics. That does not mean, you cannot use classic tools, such as the method of maximum likelihood estimation or bootstrapping, to estimate parameters and certainty intervals. However, the Bayesian approach has a number of advantages, that makes it a perfect match for New Statistics:
- The Bayesian school of thinking does not require you to imagine infinite series of replication. Parameters and uncertainty have a straight-forward interpretation: There is a best guess for the true value and there is an interval within which it lies with a given certainty. Even stronger, Bayesian models produce posterior distributions, which contain the full information on uncertainty and can be used in multiple ways. That means, we can practically always create an certainty statement that precisely matches whatever is at stake.
- In classic models, the level of uncertainty is only given for a subset of parameters, called population-level coefficients. A Bayesian model generates information on uncertainty for every parameter in the model. As a result, Bayesian models can be used to compare variance parameters between groups, or individuals within a group (so called random effects), and even correlations between individual traits. This may sound unusual and complicated, but we will see several examples of when this is very useful.
- The classic p-value also is a trick in the sense of: you can only pull it a number of times. Null hypothesis tests are available only for a very limited class of models. Bayesian tools covers a much broader class of models. For example, modelling reaction times correctly, requires a response distribution that is skewed and has an offset. Classic tools have few options for skewed response distributions, but not with an offset. Modern Bayesian engines even give you the choice out of three such distributions (such as the Ex Gaussian, see @exgaus-reg.
- Sometimes it is fully legit to ask Yes/No questions, such as: does an effect contribute to making predictions, or not? Modern Bayesian Statistics has developed a powerful toolset for what is called, model selection (8.2.4). This can either be used to test hypotheses, or to harness the shear variety of models, that can be build.
1.4 How to use this book
Chapter 1.2 introduces a framework for quantitative design research. It carves out the basic elements of empirical design research, such as users, designs and performance and links them to typical research problems. Then the idea of design as decision making under uncertainty is developed at the example of two case studies.
Chapter 3 introduces the basic idea of Bayesian statistics, which boils down to three remarkably intuitive conjectures:
- uncertainty is the rule
- you gain more certainty by observations
- your present knowledge about the world is composed of what you learned from data and what you knew before.
The same chapter goes on with introducing basic terms of statistical thinking. Finally, an overview on common statistical distributions serve as a vehicle to make the reader familiar with data generating processes. I am confident that this chapter serves newbies and classically trained researchers with all tools they need to understand Bayesian statistics. Arguably, for the formally trained reader this is more of a bedtime reading.
Chapter 2 is a minimal introduction to R, this marvelous programming language that has quickly become the Lingua Franka of statistical computing. Readers with some programming experience can work through this in just one day and they will get everything they need to get started with the book. Readers with prior R experience still may get a lot out of this chapter, as it introduces the tidy paradigm of R programming. Tidy R is best be thought of as a set standard libraries 2.0 that all follow the same regiment are therefore highly interoperable. New tidy packages are arriving at an accelerating pace in the R world, and coding tidy is usually much briefer, easier to read and less error prone, than “classic” R. While this chapter can only serve as a stepping stone, the reader will encounter countless code examples throughout the book, which can serve as exercises (1.4.3) and templates alike.
The second part of the book starts with three chapters that strictly built on each other. The first chapter 4 introduces basic elements of linear models, which are factors, covariates and interaction effects. A number of additional sections cover under-the-hood concepts, such as dummy variables or contrasts. Working through this chapter is essential for beginners as it develops the jargon.
However, for most readers, the first chapter is not sufficient to get to do some real work, as it does not cover models for more complex research designs, such as repeated measures. This is treated extensively in chapter 6. It proceeds from simple repeated measures designs to complex designs, where human and multiple non-human populations encounter each other. It culminates in a re-build of psychometric models, consisting entirely of GLMM building blocks. The chapter ends with a completely novel, yet over-due, definition of designometrics, statistical models for comparing designs (not humans).
The third chapter 7 opens up a plethora of possibilities to analyze all kinds of performance variables, that are usually considered “non-Normal” in Classic Statistics. In fact, the first part of the chapter is dedicated to convince the reader that there is no such thing as a Normal distribution in reality. Standard models are introduces to deal with counts, chances, temporal variables and rating scales. It is also meant as an eye opener for reseachers who routinely resorted to non-parametric procedures. After working through this chapter, I would consider anyone a sincere data analyst.
1.4.1 Routes
If you use this book for self study, two considerations play a role for finding the optimal route through this book. what is your background in Statistics? For using this book, effectively, you need a little bit of understanding of probabilities and basic statistics, most of which is high-school math. As such, it may be a while ago and a refresher is on order. Chapter 3.1 is a quick-read, if you are feeling confident. If you lack any background in statistics, 3 should be studied, first. If your background is Social Sciences, then you probably know quite something about probabilities and Statistics. If you wonder what all this new “Bayesian” is all about and how compatible it is to you, 3.4.4 is a small bridge.
The precondition for using this book effectively, is the skill of coding in R. If you have basic skills in another programming language, studying chapter 2 will do. If you are very experienced in programming, but not yet in R, feel confident to skip that chapter and return to it only, when you have a strange encounter. Chapters 2.2.8 to 2.2.12 explain programming techniques, where R differs the most from general purpose languages. If this is the first time, you learn a programming language, your mileage may vary. Chapter 2 can at least provide you with an overview of all that you have to know, but some other books provide a more gentle and detailed introduction to R. In any case, learning your first programming language by one book alone may turn out difficult.
All of chapters 4 through 7 have a similar structure. The first half adds a few essential techniques, whereas the remaining sections explore the depths and possibilities. If you read this book to get an overview at the first read, the recommended route is as follows:
- Section 4.1 introduces the regression engine and basic reporting techniques, such as coefficient tables
- Section 4.3.1 introduces the principles of factorial models, just enough to analyse data from an experimental design comparison.
- Section 6.3 introduces just enough multi-level thinking to get you started.
- Section 7.1 explains the three limitations of linear models, and introduces link functions and choice of random distribution.
- Section 3.5.2.4 introduces Poisson distribution as one common shape of randomness, that many people have not yet heard of.
- Section 7.2.1 puts Poisson distribution and link function to practical use on the response variable deviations
Readers approaching this book with a specific class of problems in mind, can also drill into it, like in the following examples:
Experimenters in Cognitive Psychology often use reaction time measures to test their hypotheses. The suggested vertical route matches the above up to 7.1. Then, section 7.3 introduces Exponential-Gaussian distribution as plug-in-and-use alternative to the “Normal” error term. Section 8.2.4, and 8.2.6in particular, show how hypothesis testing (and more) can be done in a Bayesian framework.
User Experience researchers (and Social Psychologists) make abundant use of rating scales. The vertical route in such a case is
- Section 4.1, 4.3.1 and 6.3.
- Section 6.5 introduces items of a rating scale as non-human populations.
- Section 6.8 shows how basic psychometric analysis can be done by using multi-level models.
- Section 7.4 elaborates on the randomness pattern of rating scales and suggests Beta regression (7.4.2)
That being said, if you are in the process of developing a design-oriented rating scale, start by reading the last paragraph of section 6.8.4!
There can also be reasons to take a more horizontal route. For example, market research often involves an insane amount of possible predictors (for when and why someone is buying a product or using a service). Sections 5 and 5.4 explore a broad set of multi-predictor models. Section 8.2.4 introduces techniques to find just-the-right set of predictors. Experimentalists, in turn, can learn more efficient ways of designing their studies by working through chapter 6, entirely. Researchers in Human Factors routinely collect multiple performance variables, such as time-on-task, number of errors and cognitive workload ratings. All these measures deserve their special way of being treated, which is emphasized in chapter 7.
1.4.2 In the classroom
Content-wise, this book covers roughly 200% of a typical Social Sciences Statistics curriculum. At least at my university, students roughly learn the equivalent of the first 50% of chapters 3, 4, 6, 7 and 8, before they graduate. However, only occasionally have I been in the situation myself, to teach a whole statistics curriculum to a cohort of students. Instead, this book emerged from statistics workshops, which I have given inside and outside universities, for professionals, colleagues and groups of master students.
If you are a docent in the Social Sciences, this book certainly can back an entry-level Statistics course. However, you should be aware that the approach in this book is not yet common ground. While you yourself may find the approach of Bayesian parameter estimation compellingly intuitive, your colleagues may not like the idea, that future generations of students perceive their work as outdated. Another consideration is that this book is only useful for students with the capacity to learn just a little bit of programming. But, do not under-estimate your students on this. I have seen it happen at my home university, that cohorts of Psychology students first started learning SPSS syntax, and now learn R and also Python. Still, using this book in te classroom poses the challenge to teach some programmingthat puts you into the situation of teaching Programming. Chapter 2 has served me well to push Psychology students over the first hurdles.
To my personal observations, there is an increasing demand to teach social science research methods to engineering students. If that is your situation, this book is particularly well-suited to make a course. Not only will programming in R not be a major hurdle, but also is this book free of outdated customs, that actually have never been appropriate for an engineering context, especially the approach of null hypothesis significxance testing. Engineers, as I know them, are interested in quantification of design effects, rather than falsifying theories. In addition, the case studies in this book convey knowledge about effective research designs and validity of measures.
In both of the above cases, if I were asked to develop a full course on the matter, I would make it a series of workshops. The most effective method for a workshop is to have students get acquainted with the matter by studying selected parts of the book, in advance, and let them work on assignments during tutored workshops. I have made good experience with tutored pair-programming, where two students work together, while the teacher stays in the background, most of the time. During each workshop, students are given a data set with a brief story to it and an assignment, like the following example:
Some novel augmented-reality (AR) side-view car mirrors have been designed and the benefits for driving performance needs to be assessed. An experiment has been conducted, where the AR mirros were compared to the classic side-view mirrors. Participants have been classified in low and high driving experience and age was recorded. Every participant completed a set of eight tasks under the following conditions:
- AR mirrors versus classic mirrors
- day ride versus night ride
The following measures were taken:
- time-on-task (seconds)
- steering reversal rate (counts, lower is better)
- cognitive workload (rating scale, 0 to 1)
Assignment:
Conceive one or more research questions, e.g.:
- The AR design creates less workload.
- The AR design improves performance especially at night
Read and clean the data set
Produce summary tables and graphs that reflect the research question
Build a model and interpret the parameter estimates.
If you use this book for teaching, that means you will have to come up with some data sets. Unless you are a seasoned researcher who can pull data out of the drawer, this might be a problem. A solution is to simulate data, like I have done multiple times in this book. While I haven’t gone to the lengths of systematically introducing data simulation, the code for all simulated data can be found in electronic resources accompanying this book.
During my workshops I often use the method of live programming. This is best pictured as think-aloud live demonstration - you talk while you are writing the code. This requires that you speak R natively, such that you can write valid code, while you talk and think. An important element of live programming is that students type the code as they see it on the presentation screen. Encouraging your students to type along, keeps them in an action-feedback loop, from head to the finger tips 1.4.3.
Examination is the other part of teaching and here is what I do in my courses: During my workshops, students get to work on a case study and for examination they get to do a data analysis on a similar case. If you prefer written exams, I advise against let students produce code on paper. Rather, I would construct questions that focus reading code, or the understanding of concepts, such as:
- Interpret the following coefficient table
- What is the difference between saturation and amplification effects?
- In which situation is it better to use an ordinal factor model, rather than a linear regression?
- Customer waiting times have been measured in several customer service hotlines. What would be an appropriate distribution family?
1.4.3 The stone of Rosetta
Next to my favorite hobby of writing books on Statistics, I am giving programming courses to Psychology students. Long have I held the belief, that the skill of coding grounds on abstract thinking (similar to learning math) and computer enthusiasm. Being a formal thinker and a nerd, are not the first things that come to mind for psychology students. Almost surprisingly, almost all of them can learn this skill within three months.
Shortly after I started working in the Netherlands, a Dutch teacher wasted my time by explaining Dutch language in English words. Only recently, a study revealed, that learning a programming language is just that: learning a second language (Prat et al. 2020). If that is true, the best way to learn it is to create a closed feedback loop. Taken to the extreme that means, every moment a programming teacher distracts a student from writing and reading code is lost.
You learn a language by being exposed to it, and that is what I will do to you in this book. Following the brief introduction to the programming language R, I will show to you every single line of code that I used to produce data, statistical models, tables and graphics. Some may find this a bit repetitive to see code for producing, say a boxplot, over and over again. I beg to differ: for learning a language, repetition is essential.
Before I came to the Netherlands I lived about ten years in a southern part of Germany where many people speak a strong dialect, Bayrisch. Surprisingly, I am better at speaking Dutch than I ever were at this dialect. Maybe, this is because Dutch people react cheerful when you try in their language, whereas people from Bayern hate it, when you imitate their way of speaking. (The trick I found most useful for doing a half-way acceptable imitation is to imagine a native-speaking friend and how he would say it.) When learning R, no one will laugh at you when you struggle to express yourself. And the same trick works here, too: If you want to produce or express a certain result, just flip through the pages of this book and you may find a piece of code where I “said” something similar. Cutting-and-pasting is a basic form of a fundamental principle of good coding: maximizing re-use.
The importance of closed-loop interaction holds even stronger, if the skill to be learned is a language. This book is written in three languages: English, R and here and there a little bit of math. Precise description a chain of data processing is difficult to do in a fuzzy natural language, like English (or Dutch). R, like math, is a formal language, and every piece of code will always produce the exact same result. The difference between math and R is that math is purely descriptive (or rather, imaginative), whereas R not just productive, it is also interactive. You can specify a Gaussian distributed variable in math, by saying:
\[ \begin{aligned} \mu &= 7\\ \sigma &= 3\\ Y &\sim \textrm{Gauss}(\mu, \sigma)\\ \end{aligned} \]
Or, you can produce such a variable in R:
Data_gaus <- tibble(y = rnorm(n = 1000, mean = 3, sd = 5))The math expression requires that the recipient of the message can imagine how a Gaussian distribution looks like. In R, you can simply show, how it looks like (Figure @ref(fig:data_gaus_1)):
Data_gaus %>%
ggplot(aes(x = y)) +
geom_histogram(bins = 12)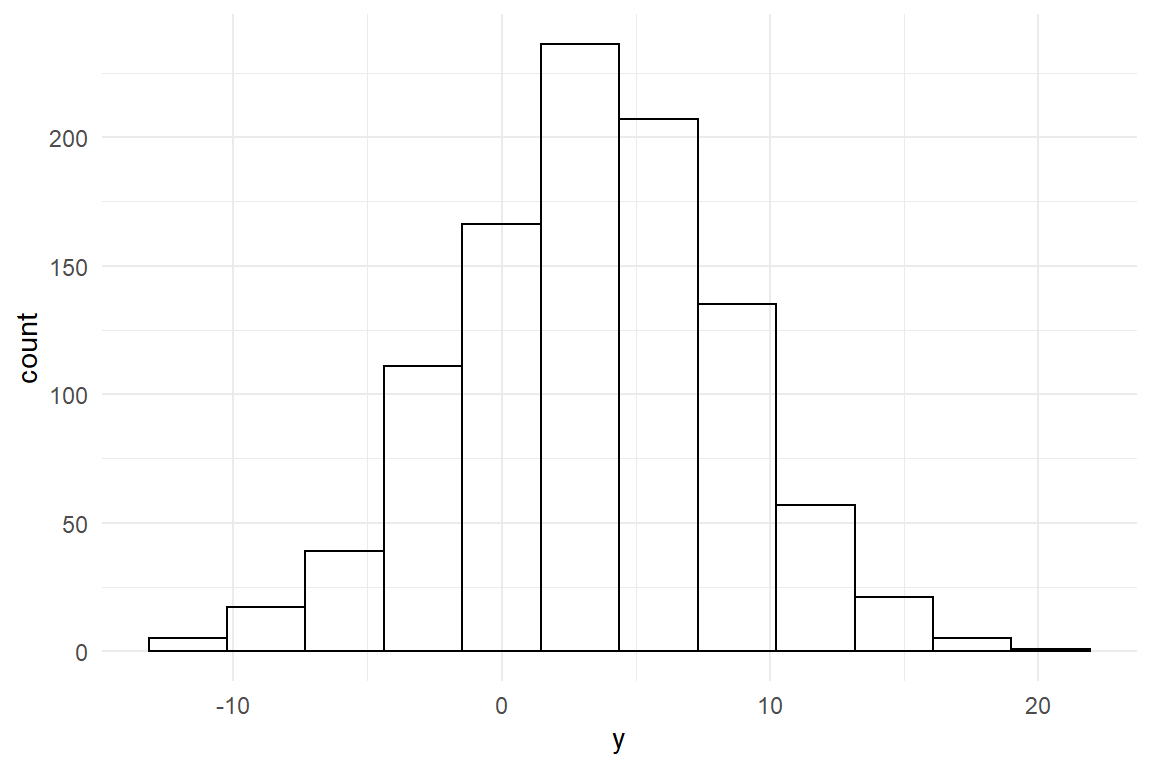
Figure 1.1: A Gaussian distribution
In many other books on statistics, math is used to precisely specify a model or any other data transformation. Specifying how data has been processed is essential for transparency of research. In the ideal case, data processing is given as a recipe so precise, that every other researcher would obtain the exact same results. That is called re-producability. Math notation lives up to the principle of transparency, but most people do not have the skills, to produce something from math notation. Speaking for myself, if someone would ask me for the formula of Gaussian distributions from the top of my head, I would be in trouble:
\[ P(x) = \frac{1} {{\sigma \sqrt {2\pi } }} e^{{{ - \left( {x - \mu } \right)^2 / 2\sigma^2}}} \]
Because math is such an inaccessible language, in practice, math notation is hardly reproducable, whereas R code is. If anyone gives me their R code and the data, I can expect to get the exact same results. If I apply the code to my own data, I am doing an exact replication of a study. On top of that, I will always be able to check the validity of every single step in the analysis, as I will demonstrate below.
The principle of transparency in scientific reports requires the author to specify all
- transformations that have been acted out on the data
- tables and figures that are presented
- assumptions of statistical models
Traditionally, specification of figures and tables is done by putting text in captions. While English texts may please a lot of readers, this has disadvantages:
- A table or figure is the result of complex data transformations, which are difficult to put in words, precisely. Sometimes, important details are given in other parts of the document, or are just lost. An example is outlier removal.
- Describing what a figure or table shows, does not put the readers into the position to reproduce or replicate the table or figure.
For these reasons, I decided to spare any caption texts on figures and tables in this book. Instead, all results presented in this book, are fully specified by the R code that produces them. From a didactic point of view, I am deliberately taking away the convenience that may come with natural language, for putting my readers’ brains into an action-feedback loop. All R code in this book has been crafted to specifically serve this purpose. In particular, all code snippets are written as data processing chains, with one operation per line. The best way to understand the code at first, is to run it starting at the top, examine what the first transformation did and then include the next step:
set.seed(47)
tibble(y = rnorm(n = 20, mean = 2, sd = 5)) %>%
as_tbl_obs()| Obs | y |
|---|---|
| 1 | 11.97 |
| 5 | 2.54 |
| 8 | 2.08 |
| 10 | -5.33 |
| 14 | -7.14 |
| 16 | 5.35 |
| 19 | -1.52 |
| 20 | 1.80 |
set.seed(47)
tibble(y = rnorm(n = 20, mean = 2, sd = 5)) %>%
as_tbl_obs() %>%
filter(y > 0)| Obs | y |
|---|---|
| 1 | 11.97 |
| 3 | 2.93 |
| 5 | 2.54 |
| 12 | 2.20 |
| 13 | 4.47 |
| 16 | 5.35 |
| 18 | 8.32 |
| 20 | 1.80 |
set.seed(47)
tibble(y = rnorm(n = 20, mean = 2, sd = 5)) %>%
as_tbl_obs() %>%
filter(y > 0) %>%
ggplot(aes(x = y))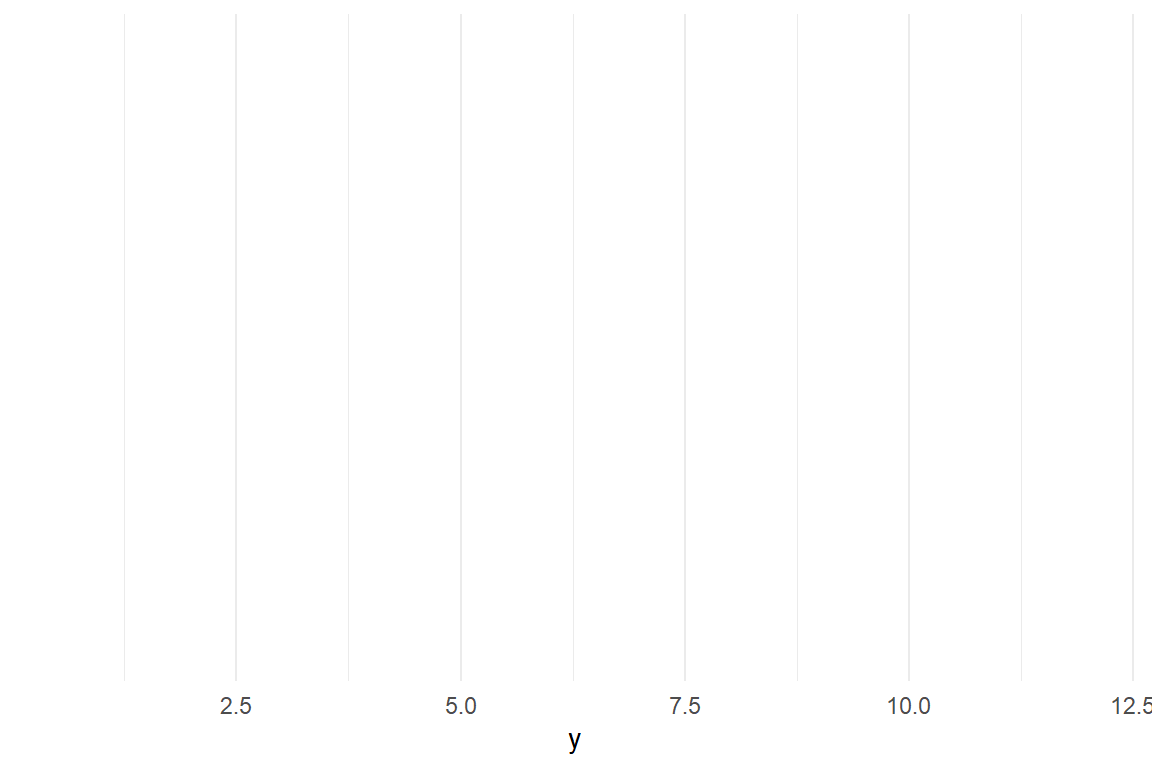
Figure 1.2: Piping data into the plotting engine
set.seed(47)
tibble(y = rnorm(n = 20, mean = 2, sd = 5)) %>%
as_tbl_obs() %>%
filter(y > 0) %>%
ggplot(aes(x = y)) +
geom_histogram(binwidth = 2)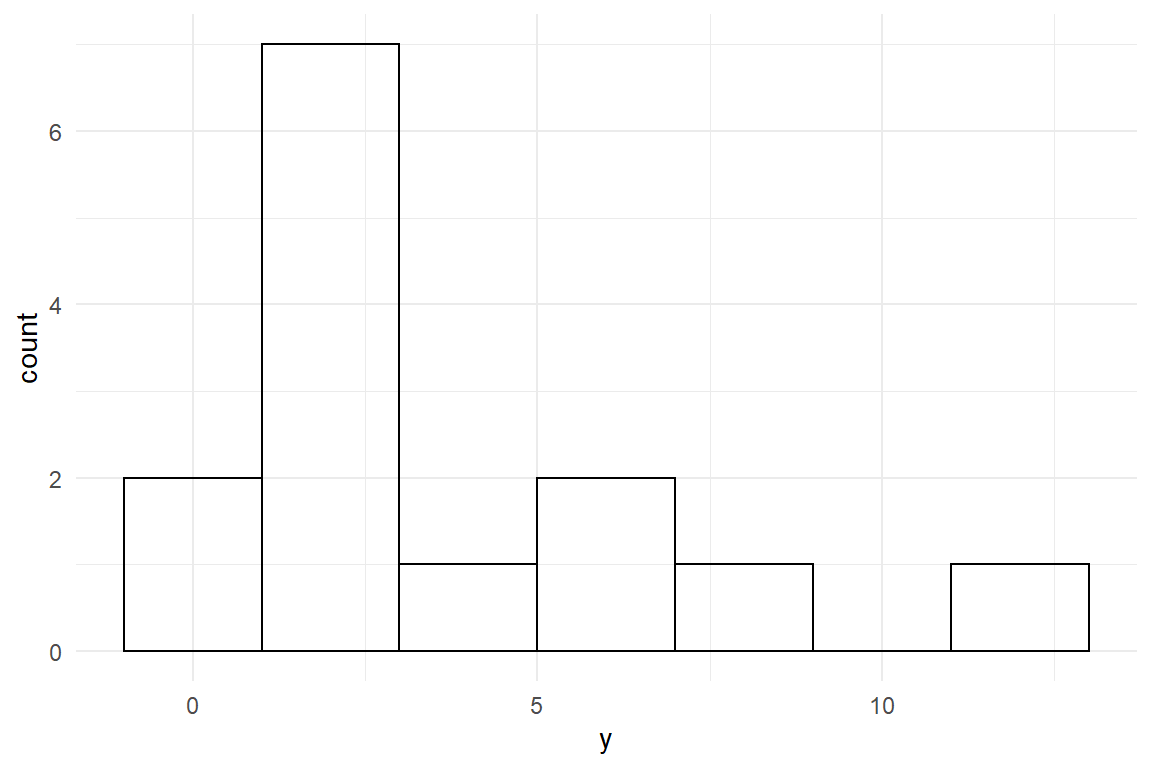
Figure 1.3: Plotting a histogram
It is almost obvious that changing mean = 2 changes the mean (Table 1.1) of the distribution ß, and that filter(y > 0) removes non-positive values (Table 1.2). The real fun starts when the Ggplot graphics engine is loaded with data. In Figure 1.2 you only see an empty coordinate system. In Figure 1.3 a so called geometry is added, creating a histogram.
And this is not the end of the story. Rather, it is the beginning of another phase in learning to programming, where you start working with existing code and modify it to your needs. The ggplot graphics engine in particular is easy to learn and, yet, provides almost endless possibilities to express yourself in a report. It is also very well documented. With some googling you will quickly find a recipe to add a properly scaled density line to the plot (Figure 1.4):
set.seed(47)
tibble(y = rnorm(n = 20, mean = 2, sd = 5)) %>%
filter(y > 0) %>%
ggplot(aes(x = y)) +
geom_histogram(binwidth = 2) +
geom_density(aes(y = 2 * ..count..))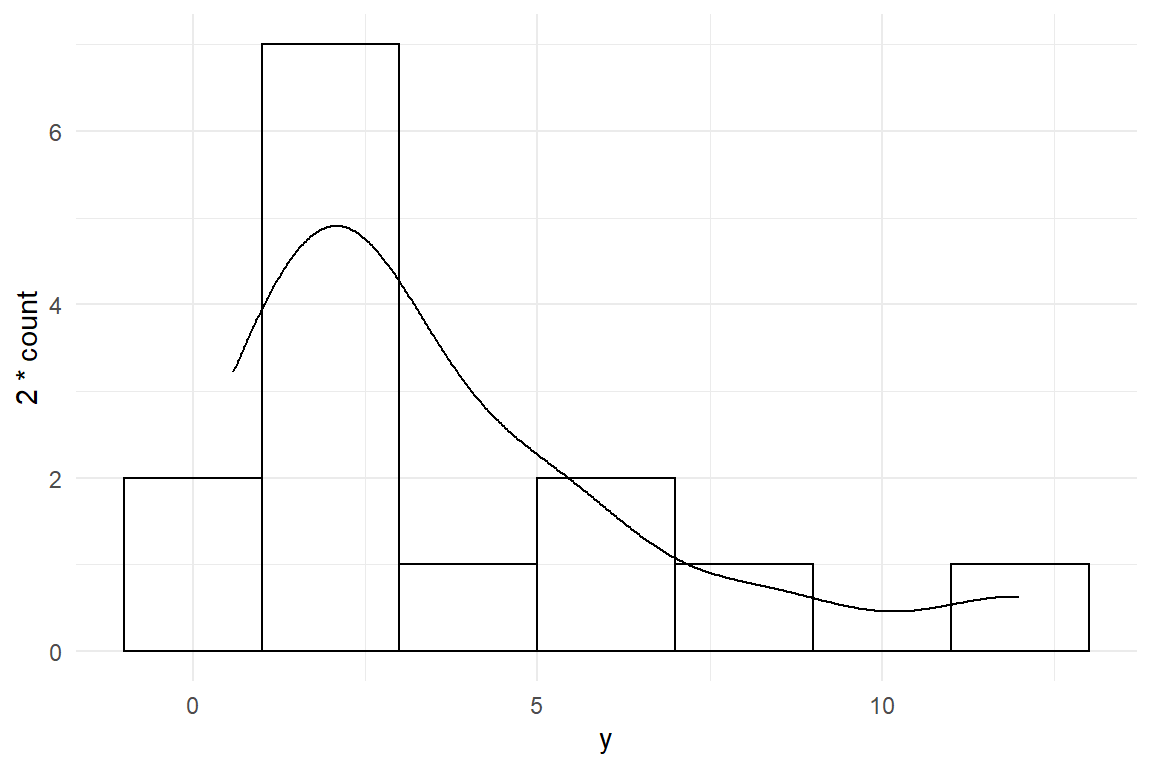
Figure 1.4: Adding another layer
In contrast to math notation, R is productive and that opens new ways for learning statistics. Several chapters will make use of a technique best described as generation-and-recovery, where a data generating process is expressed as a simulation function and the result is recovered by a matching model. Loop closed!
1.5 Thank you and supplementary readings
To keep the book lean, I refrained to use citations a lot. That does not mean I was independent. The opposite is the case and the following authors greatly influenced my way of thinking and I certainly copy-catted more than I am aware of. Thank them for the inspiration!
(Gelman and Hill 2006) is the oldest Statistics textbook I still have in use. Not only was it the first one of its kind to promote the programming language R, it also develops a similar framework of models and already introduces a few Bayesian
(McElreath 2018) is targeted at statistical users, who are so deeply stuck in the Classic Statistics paradigm that they need a proper therapy. In an informal language, it covers theoretical and philosophical issues of Bayesian Statistics at a great of a depth and is fully compatible with New Statistics. This was the one book that inspired me to replace mathematical formalism with code.
(Doing Bayesian Data Analysis 2015) is another highly regarded in this league of Bayesian textbooks. For professional academic researchers, this book is a valuable addition, as it is more profound, comes with a comparably huge bibliography and translates the NHST framework into Bayesian language, rather than dismiss it entirely.
(Lee and Wagenmakers 2009) is a Bayesian journey through Cognitive Psychology. Like no other book it demonstrates the knowledge-driven process of translating research question into statistical models.
(Gelman et al. 2013) simply is the reference in Bayesian applied statistics. Many aspects of Bayesian analysis, that the present book and others in its league rather illustrate than justify, are explained and discussed with exquisite detail.
Then, I want to thank all former students who have collected the data sets I am using: Jop Havinga, Cornelia Schmidt, Lea Echelmeyer, Marc Danielski, Robin Koopmans, Frauke van Beek, Raphaela Schnittker, Jan Sommer, Julian Keil, Franziska Geesen and Nicolas Sander.